Next in my Blog series on olden Indian Mathematicians and scientists is T Sundar Rao. He spells Rao as Row. His book called Geometric Exercises in Paper Folding was published in Madras (now Chennai) in 1893. As the title states, Sundara has demonstrated many geometric shapes and equations by using simple paper and by folding the paper in different ways to create creases that will define the geometric shapes. This book is available in Amazon and Flipcart for general purchase.
Tandalam Sundara Row was born in 1853 in Tamil Nadu. He was the son of a college principal. He completed a bachelor’s degree at Kumbakonam College in 1874. Kumbakonam is a small town south of Chennai,closer to Thanjavur. He scored only second-place honours in mathematics and was always fascinated by mathematics. After graduation, he got a British Indian Government Tax collector civil service job. However, even with a full-time job, he did spend time on his passion for mathematics as an amateur. He published his first book, our Blog Topic, in 1893, and a second book on mathematics called the Elementary Solid Geometry, published in three parts from 1906 to 1909.
How did Sundara get the idea or inspiration to write this book?
He read and liked the book written by another Kumbakonam College Teacher. The book was First Lessons in Geometry by Professor Bhimanakunte Hanumantha Rao 1855-1922. Hanumanta Rao started his career as an Assistant Master in the same Kumbakonam College and retired as a Professor of Mathematics at the College of Engineering Madras.
Another book that inspired him was from Friedrich Froebel, 1782-1852, a German widely known as the Father of the Kindergarten. He believed that the whole knowledge is inherent in man, it is the function of the teacher to bring it out. The children are given such an environment in kindergarten schools to make them aware that they learn by doing. His emphasis was on activity, doing it on your own, and seeing the results. One of his Children’s games sold as a gift was called Kindergarten Gift No. VIII: Paper-Folding. This was a game encouraging children to fold papers in different shapes and understand shapes etc. This gift inspired Sundara Rao to take it to the next level and explore paper folding for simple to complex geometrical shapes and also prove mathematical formulas.
Geometric Exercises in Paper Folding was first published by Addison & Co. in Madras in 1893. The book became a success in Germany thanks to Felix Klein who referred to it in his Geometry book in 1895. The Open Court Press of Chicago published it in the US listing four editions in 1901,1905,1917 and 1941. The last edition was published by LaSalle, London also.
Now get us to get into the book. At a very high level, this book suggests the use of simple folding of paper creating visible creases to draw various geometric figures instead of classical Greek straightedge and compass constructions. Let us not get swayed by the Kindergarten game influence and assume this book is for easy mathematics. This book
covers very complex geometric shapes such as Polygons and covering major theorems such as Pythagoras’ theorem, Desargues’s theorem, Pascal’s theorem, and Poncelet’s closure theorem. The book has 285 exercises with illustrations and even pictures of the paper folds.
In this post, I will be covering a few simple geometrical structures involving rectangles, and squares and stop at the famous Pythagoras’s theorem. Interested readers can purchase the book and learn a lot more complex areas.
Sundara starts the discussion with how to cut a rectangle from any oddly shaped paper. I will skip this as most of the paper available now are already cut in a rectangle shape.
The first example I am covering here is to create a square of smaller side of the rectangle from a rectangle by two folds.

Step1 : Take the smaller side of the rectangular paper and fold on to itself.
Step2 : Use the excess below and fold it along the horizontal edge
Step3 : You are done. You can see the crease indicating the square edge and you have a square figure with same length as the smaller side of the original rectangle.
Let us look at what we can do with the squares.

Let us look at picture 1 .
We have folded the square multiple times and created many smaller squares. We can see 4 smaller squares of quarter size of the original square. We also see 16 even smaller squares 4 in each row and 4 rows. Easy to agree that each square if 1 /16 size of the original square. Also each smallest square of divided into 2 congruent triangles each having an area of 1/32 size of the original square.
Now let us look into the black outlined square with a slightly rotated view. This is created by just simply folding the paper across each of the 4 midpoints of the original square. Just count the smallest triangles inside the square. You will see 16 of them. Hence the square is half the size of the original square. 16 * 1/32 = 1/2.
Let us go one more level deeper. Look at the crease connecting the midpoints of the inner 4 squares creating e a new square red-lined in the picture. This red lines square has 8 triangles
and hence a quarter of the original size. 8 * 1/32 = 1/4. This is also half of the previous square which was ½ the size of the original square.
Conceptually we can go on repeating this and create smaller and smaller squares with each new smaller square half the size of the previous squares. In each iteration we are leaving half the area of the triangles and using up the other half. Hence, the sum of all these triangles in the squares cannot exceed the original square and must eventually become the original square. if we add all the squares up, it will be the same as the original square.
Assume the original square if 1 unit size and area is 1. Then we can deduce this formula
½ + ¼ +1/8 +1/16 ….. up to infinity = 1
Or
½ +1/2 2 + 1/2 3 + 1/2 4 ….. up to infinity = 1
This series has been of interest to many philosophers around the world. Zeno a Greek Philosopher 490-430BC has written many philosophical problems as paradoxes and one of them called Archilles and Tortoise Race ponders about this sequence.
The paradox is as follows:-
The warrior Achilles was to race against a tortoise. The track is 100 meters long. Achilles could run at 10 meters per second while the tortoise only 5. However, the tortoise is given a 10-meter advantage. Zeno argued that the tortoise will always win. He argued that Achilles would have to move 10 meters to catch up to the tortoise to cover the advantage starting point, but by then the tortoise would already have moved another five meters. Achilles would then have to move 5 meters, where the tortoise would move 2.5 meters, and so on. Zeno argued that the tortoise would always remain ahead of Achilles.
Even early Chinese Taoist philosophers pondered this question. In an ancient book Zhuangai, we see this puzzle. “Take a chi long stick and remove half every day, in myriad ages, it will not be exhausted.”. Every day you will have a stick half the size of the earlier day but you will always have some stick and you can never get rid of the stick.
It is so great to see our Sundara Row solving this philosophical problem by simple folding. He showed that sum of all these squares however many you create has to be equal to the original square and resolved the paradox.
Second illustration I want to show in this post is our grand old Pythagoras theorem. You saw it in my earlier two posts also.
Just to recall, Pythagoras’s theorem says for a right-angle triangle, the square of the hypotenuse is always the sum of the squares of each side.
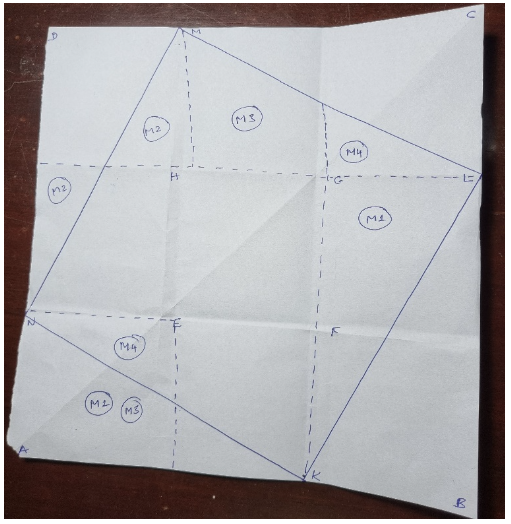
Please see the picture above.
Step 1 : Create a 3 x 3 folds to create 9 squares.
Step 2 : Fold from first horizontal divide point to 2 nd vertical divide point.
Step3 : Repeat 3 times to complete the rotated square KLMN.
Let us focus on right angle triangle AKN to prove Pythagoras theorem.
We all agree that KN is the hypotenuse and the thick line rotated square KLMN area is the square of the hypotenuse.
We also agree that the smaller dotted line square area below NE is the square of one side of the triangle. We also agree that the bigger dotted line square on top of AK is the square of the 2 nd side of the triangle i.e. AK.
Now let us see how we cut and move things around to combine the two dotted line squares to get the rotated thick line square. This will prove the Pythagoras theorem.
You can see that AK dotted square is inside the thick line rotated square except for two shapes marked M1 and M2. We have to find space for these missing pieces inside the KLMN rotated square.
What is missing from the NE smaller dotted square? The area marked M3 with the dotted line as the side boundary. Also, the shape marked M4 is common between the two dotted line squares. This needs to be accommodated twice to get the sum of the areas correct.
We can see in the pictures, how M1, M2, M3, and M4 are accommodated to create the rotated KLMN square. Such a simple ingenious way to prove the Pythagoras theorem.
As I have said before these are just the first few folding examples and the book is very complex and explains many complex geometric principles and theorems up to higher secondary and even under graduate college levels of education.
The intent of the book was both to become aid for geometry teaching at schools and also be a
work of recreational mathematics to attract general audience in to mathematics & geometry. While they were few critiques, predominantly mathematics educators appreciated the book. Pamela Liebeck a mathematics educator remarked that this book is remarkably relevant to the discovery of learning techniques of geometry of the time. According to Michael Friedman, a historian of mathematics, the book has become “one of the main engines of the popularization of folding as a mathematical activity”. As late as 2016, Computational Origami expert Tetsuo Ida wrote “After 123 years, the significance of the book still remains”.
I hope with this brief book summary I have been able to get you all interested to read more. As I have said before, Book is available for purchase.
More later.
L Ravichandran

