Hope you all liked my Blog on Poththanar and as I promised I am ready with my 2 nd Blog on the same topic. I will be talking about Baudhayana, a Vedic scholar, philosopher, and mathematician who wrote in the Sanskrit language. Baudhayana lived in the 800 BC – 740 BC era, almost three thousand years ago.
He wrote a group of Vedic texts in Sanskrit called Baudhayana Sutras which cover various topics to help citizens to live their lives and perform religious rituals.
Surprisingly one of the texts includes detailed mathematical formulas to help in large constructions of palaces, temples, dams, cities, etc.
The Baudhayana sūtras consist of six texts:
- Srautasutra is about performing Vedic rituals and sacrifices.
- Dharmasutra is the book of law. The sutras talk about social classes, the role of the king, marriage, penances, inheritance, women, householder, orders of life, and ancestral offerings.
- Karmantasutra, Dwaidhasutra, and Grihyasutras talk about the duties of all citizens, domestic life, etc.
- Sulba Sutra contains mathematical formulae used for practice applications.
The Baudhayana Sulbasutra is the topic of interest for this blog. Vedic philosopher scientists were more focused on the application of geometry, and mathematics for practical use than generalization and providing universal proof of the theorems or formulae. They seem to have used the formula for various practical applications and verified that this is working correctly for these situations. They never bothered to generalize and offer proof of these formulas. They were stated as Sanskrit slokas and accepted and used by builders and engineers to cut stones, build monuments, etc.
I am sure many of you have visited ancient palaces, ruins of old cities, and large temple complexes and wondered about the sheer complexity, size, and mechanics of building these with the old set of primitive tools. One aspect which strikes all is the use of geometric shapes. We see the use of basic geometric shapes such as squares, rectangles, triangles, circles, and rhombus all around these monuments.
How did the building engineers calculate the length of hypotenuses or diagonals or the area of the circle when Pythogarus who invented Pythagoras theorem was yet to be born and concepts like the Square root of 2 or Pi were thousand-plus years away to be discovered. ? They simply used the Badhayana Sulbasutra formulas and got the job done. Astonishing isn’t it?
I will highlight a few sulba sutras to give you a feel of Baudhayana’s geometry and mathematical knowledge.
Square Root of 2 , is a basic mathematical number needed to do calculations on measuring the diagonal of a square or a rectangle or a hypotenuse of a triangle. We know now that the length of a diagonal of a square with length 1 is √2.
The actual text in Sanskrit is as follows:-
Samasya dvikaraṇī. pramāṇaṃ tṛtīyena vardhayet
tac caturthenātmacatustriṃśonena saviśeṣaḥ
A rough English Translation will be
The diagonal of a square. The measure is to be increased by a third and by a
fourth decreased by the 34th. That is it’s diagonal approximately.
The formulae derived using the sulba sutra text is
Diagonal of a square of 1 unit i.e √2 = 1 + 1/3 + 1/(3*4) – 1/(3*4*34)
√2 = 1 + 0.33333 + 0.08333 – 0.00245 = 1.41421.
The result is matching with current calculations up to 5 decimals accuracy.
I have taken a square of 1 unit to illustrate. The formula will work for any length square.
For example, let us take a square of length 5
Diagonal length = 5 + 5/3 + 5/(3*4) – 5/(3*4*12)
= 5 +1.66666 + 0.41666 – 0.01225 = 7.07107
= 5 x √2
Now let us look at some interesting formulae for triangles and rectangles. We all know that diagonal of a rectangle or a hypotenuse of a triangle follows the same logic.
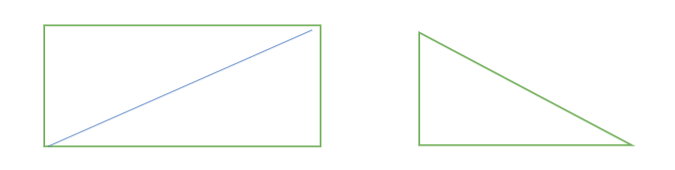
Baudhayana Sulva sutra text describing properties of the two sides of a triangle or a rectangle and the diagonal/hypotenuse is as follows.
dīrghachatursrasyākṣaṇayā rajjuḥ pārśvamānī, tiryagmānī,
cha yatpṛthagbhūte kurutastadubhayāṅ karoti.
A rough English translation will be
The diagonal of an oblong produces by itself both the areas which the two sides of the oblong produce separately.
The two sides referred to are interpreted as two sides of a rectangle or a triangle.
The diagonal is the diagonal of a rectangle or the hypotenuse of a right-angle triangle.
The formulae says Hypotenuse area = side1 area + side2 area ;
Same as the famous Pythagoras theorem c2 = a2 + b2 who lived around 570 BC to 500 BC, 200 years later than Baudhayana!.
Baudhayana also gives an easier formula for the special case of a square or a triangle with equal two sides. He refers to a common tool used by building engineers of those days, a string or a chord for measurement.
The Sulab sutra text is translated as follows:-
The cord which is stretched across a square produces an area double the size of the original square.
The stretched cord across the square will be along the diagonal and hence the formulae derived from the text is
Diagonal of a square2 = 2 x square length2
This is a special case of Pythagoras’ theorem for isosceles triangles.
Baudhayana also gives an approximate formulae for calculating the diagonal or the hypotenuse.
Let a and b are two sides , with a being the larger side. Let a also be divisible by 4.
Hypotenuse c = ( a – a/8) + b/2.
We have seen the same formulae promoted in Tamil by Pottanar, which I talked about in my previous Blog.
Another interesting geometric shape of interest is the circle. Mathematicians always wondered about the relationship between the circumference and diameter of a circle.
They experimented with many circles and agreed there is a constant that is common across all circles which now we call Pi or π.
Now we all know now that a. radius is half the diameter and b. the circumference is 2π r and c. the area of the circle is π r2 . The value of Pi or π always intrigued all. It is usually attributed to Archimedes 287 BC – 212 BC.
Baudhayana attempts to solve this Pi mystery in two ways. He experimented with many circular shapes of different dimensions and suggested 3 different approximations to be used for building applications. He suggested 676/225, 1156/361 or 900/289. All three are good approximations and useful for building engineers of those days.
Another ingenious way, he attempted to solve this Pi problem is to find a circle whose area is the same as a square. Then by calculating the area of the square which is the same as the circle, one could reverse calculate the value of Pi / π.
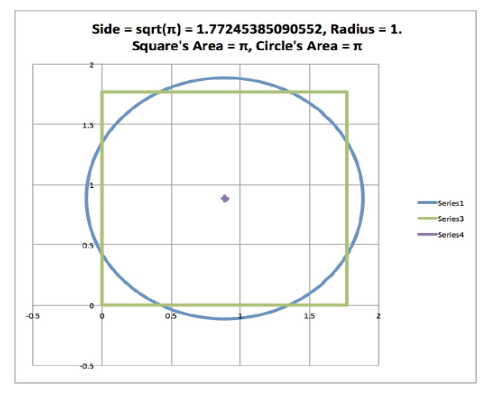
The English translation of the sulab sutra text for finding this circle is as follows
“Draw half its diagonal about the center towards the East-West line; then describe a circle together with a third part of that which lies outside the square”.
Let me explain this formula using simple numbers. Assume the square is of length
1.
- The area is the square is 12 i.e 1 ;
- Diagonal of the square as per Baudharyana formulae is 1.414.
- Half of the diagonal length is 0.707. half of the side length is 0.5
- Lying outside the square is 0.707 – 0.5 = 0.207.
- 1/3 of lying outside the square is 0.069.
- Radius of the circle with the same area is 0.5 + 0.069 = 0.569.
- Reverse calculation of π is π = 1 / ( 0.569*0.569) = 3.088
Another interesting geometric shape for construction is Rhombus. Baudhayana experimented with various rectangle middle points to create rhombus shapes and wrote these conclusions.
- Diagonals of a rhombus bisect (with equal length on both sides) and also at right angles.
- Diagonals of a rectangle bisect each other.
- Rhombus created by connecting the midpoints of a rectangle is half the area of the original rectangle.
Again, Baudhayana does not offer any proof or generalizations that these formulae will work in all circumstances. The emphasis on square, circle, rectangle, triangle, and rhombus is due to the need for these shapes in all forms of monument construction including the prayer altar ( Yajna bhumikas) on which all Vedic rituals are conducted.
After reading this blog, I am sure you can appreciate how the builders cut their stones with precise fittings to create shapes, estimated the quantity needed to fill up the geometric shapes, etc. It is very unfortunate that these great mathematicians’ findings were not publicized across the world and all of these formulae got attributed to other Western philosopher mathematicians like Archimedes or Pythagoras etc.
I also wonder what made these philosopher mathematicians stop at approximate estimates for practical applications and not look for generalized proof of these algorithms.
A lot more wisdom was there during Vedic times and wait for my next blog on this topic soon.
Author: L Ravichandran

