Pothanayur lived around 800 BC i.e 2800 years ago and worked on many solutions to help the construction of dams, temples, and palaces which need measurements of various shapes.
Lately, there are lots of discussions and excitement about Potanayur’s simpler alternate solution to the famous Pythogarus Theorem which is used to measure the hypotenuse of a right-angle triangle.
Refer picture below.
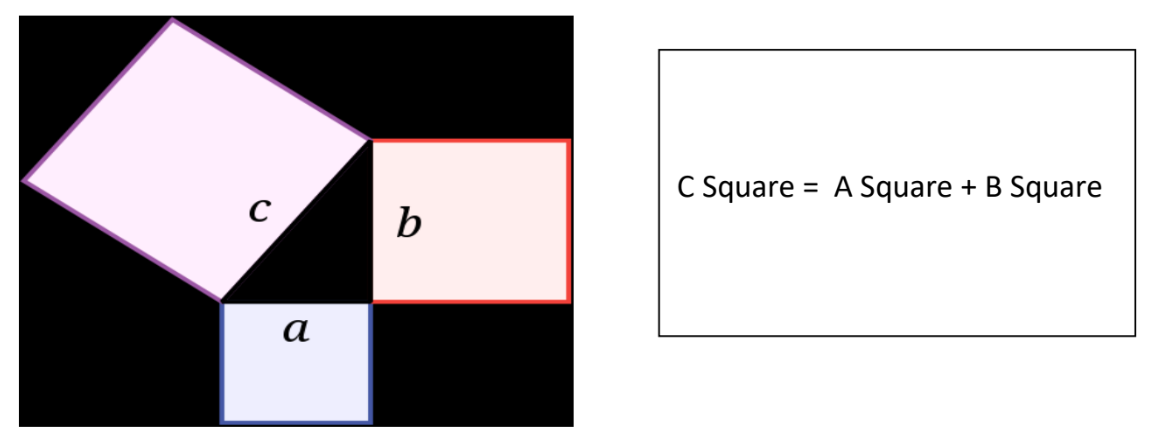
Pythagoras was born in 570 BC and developed this famous equation named after him. He basically postulated that the sum of the squares of both the sides is same as the square of the hypotenuse for all right-angle triangles.
Even before Pythogarus, Indian mathematicians wrote The Baudhayana Sutras consisting of various mathematical formulae. The Baudhayana Sutras written in Sanskrit cover a broad range of topics such as dharma, daily ritual, laws of the land, and mathematics. It is dated to 1st millennium BC and is one of the oldest Dharma-related texts of Hinduism that have survived till now.
The rule for calculating hypotenuse of a right angle triangle as written in the Baudhāyana Sulba Sūtra is as follows.
“dīrghachatursrasyākṣaṇayā rajjuḥ pārśvamānī, tiryagmānī, cha yatpṛthagbhūte kurutastadubhayāṅ karoti.”
Roughly translated as “The diagonal of an oblong produces by itself both the areas which the two sides of the oblong produce separately.

The diagonal line is referred to as the oblong and two sides of the triangle are the two sides mentioned. The statement says the area created by both sides put together is the same as the area created by the oblong. Exact equivalent of the famous Pythagorean theorem. This text is dated before Pythagoras.
Another interesting corollary theorem of isosceles right-angle triangle i.e. right angle triangle with both sides are the exact same length. As per Pythagoras’ theorem, the area of the hypotenuse will be double the square of the side.
The Baudhayana uses a rope analogy and the formulae is written as below.
The cord which is stretched across a square produces an area double the size of the original square.

Isn’t to astonishing to see such great mathematical thinking in India during Vedic times. I will write a detailed blog on Baudhayana later and let us get back to Pothanayur.
In olden times, dams, massive temples, and palaces were built with granite and other stones and require exact measurements for cutting the stones and fitting them. To calculate the exact length of the hypotenuse of a right-angle triangle, we need to
- Square the two sides and add them, which is easy.
- Calculate the square root of the above sum, which was difficult
Pothanayur was a philosopher, poet, and mathematician who lived around 800 BC. He found a simpler calculation without involving square roots to solve the problem of calculating the hypotenuse length. His original wordings in Tamil were
“Odum Neelam Thanai Oreettu Coory aakki Coorile ondrai thalli
Kundrathil Paadhiyal chertaal
Varuvathu Karanam thane
“Roughly translated as Take the longer side and divide it into 8
Remove 1/8 from the longer side length
Add half of the shorter side length
You get the length of the hypotenuse.
Let us assume A is a larger side and B is the smaller side of the right-angle triangle. Pothanayur formulae is
Hypotenuse C = 7/8 A + 1⁄2 B; No square, No square root. Using only single fractions and addition.
We can try it out with a few numbers and this gives the exact same result as the Pythogarous theorem. For example, let us take A = 8 and B = 6.
As per the Pythogarous theorem, 88 = 64 + 66= 36 = 100; the square root of 100 is 10.
As per Pothnayur formula, 7/88 = 7 , 1⁄26 = 3 , 7 + 3 = 10. Exact same answer.
The exact results are achieved for many more numbers. However, this formula has some drawbacks. When the shorter side is very short compared to the longer side (e.g. 10000 versus 5 ), then the Pothanaur formula will fail. These examples of very thin triangle shapes were not required in the olden constructions and this formula worked well in practice. The wordings are very clear to take a larger side as A and the shorter side as B in the formulae which are missed by many people who criticize the formulae.
I am not saying that this is a replacement for the pythogarous theorem. However, I wanted to highlight that these mathematical problems were researched by scholars in the Vedic period and each had come out with workable solutions for the need of the day.
Let us recognize and applaud Pothanayur for his contributions to mathematics and engineering.
Author: L.Ravichandran